LLMs are secretly good at regression calculations
If you know the special way to prompt them, that is.
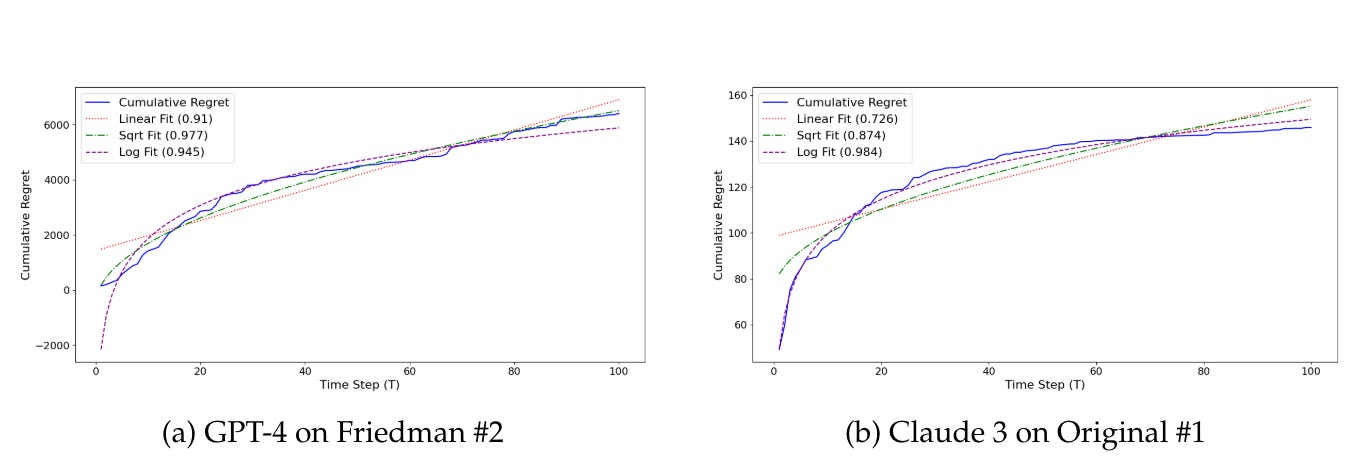
“Figure 7: The cumulative regret of two large language models on two different non-linear regression dataset. Both show a sub-linear regret grow, indicating that as more data points are observed, the models become increasingly efficient at predicting outcomes closer to the optimal strategy derived in hindsight.”
Can an AI system designed for language also excel at math? One of this week’s hottest new studies suggests the answer is yes.
This finding could upend our basic assumptions about AI - namely, that optimization linguistic token prediction limits the usefulness of LLMs for math. In this post, we’ll take a look at:
What the researchers actually did and discovered
How language models seem to "learn math" as a side effect of how they work
What it means for the future of AI in data science and beyond
Overview
Researchers at the University of Arizona and Technical University of Cluj-Napoca tested state-of-the-art AI language models like GPT-4 and Claude on a variety of mathematical curve-fitting tasks. The results were stunning: the language models matched specialized machine learning systems at finding patterns in data points - without being designed for it.
Normally, to find mathematical patterns in data (like fitting a line to a scatter plot), you train a specialized machine learning model. A data scientist carefully selects a model type suited for the kind of data relationship they expect (e.g. linear, polynomial, etc). They feed the model a bunch of example data points and tweak parameters until it fits the points well - a process called training.

Go watch the video if you haven’t yet, it’s so smooth.
What this new study suggests is that massive general-purpose language models can essentially do the same thing out of the box. The researchers tested language models like GPT-4 and Claude on tasks like:
Fitting a straight line to data points (linear regression)
Fitting curvy lines to capture more complex relationships (polynomial regression)
Approximating various tricky mathematical functions
In theory, language models shouldn't be good at this - they're designed to predict the next word in a sentence, not to do math. But the researchers found that the language models matched or even beat classic models designed for curve fitting, like linear regression, random forest, and support vector machines.
Here's the kicker: the language models did it without any special training or tweaking. They weren't fed model parameters or loss functions. They just looked at example input-output pairs and figured out the pattern, the same way they look at word sequences and figure out what word comes next.
This suggests that as language models get better and better at mimicking human writing, they pick up other cognitive skills as a side effect - like an intuitive sense for numbers. They learn "the language of math" without being taught.
Now let's dig into the details of the study and what this finding could mean for AI, data science, and our understanding of intelligence.
Related reading: AI discovers new solutions to two famous math problems.
Plain English Explanation
Data scientists use math to find patterns in messy data. They usually do this with specialized tools that they have to carefully set up and train with specific instructions. Kind of like training a dog to do an obstacle course.
What this study found is that AI language models - normally used for writing and analyzing text - can find these mathematical patterns too, just by roughing it. Somehow, in learning to recreate human language, it picks up other skills on the side.
So in practice, this could make data analysis and number crunching a lot faster and easier. Instead of having to train a bunch of specialized models and compare them, you might just be able to throw a massive language model at a dataset and have it spit out the patterns.
More broadly, it suggests that as AI language models get more sophisticated, they're not just getting better at writing - they're getting smarter in a more general, human-like way. They can connect the dots and spot hidden relationships, even in fields they weren't explicitly designed for. It's a step towards more flexible, adaptable AI.
So while this study is focused on a niche area (curve fitting), it provides a glimpse of a possible future where AI can fluidly move between different modes of reasoning - language, math, logic, etc. - without hard boundaries. Where intelligence isn't a bunch of narrow specialties, but a general capacity to learn and infer.
Pretty wild stuff. Now let's look at the nuts and bolts of how they showed this.
Technical Explanation
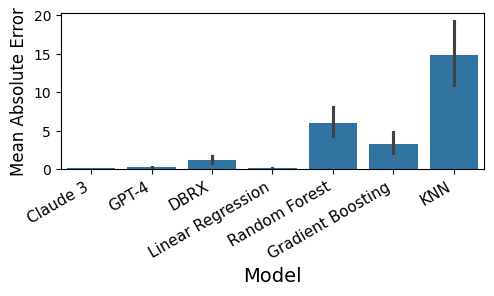
Comparing performance of Claude 3, GPT-4 and other approaches. Figure 1 in the paper.
The researchers took a bunch of different language models (GPT-4, Claude, etc.) and put them through their paces on a gauntlet of regression tasks. Regression just means finding a mathematical function that fits a set of data points. The tasks varied in complexity:
Linear regression:
Fitting a straight line (e.g. y = 2x + 3)
With 1-3 input variables
And 1-3 variables actually being predictive
Nonlinear regression:
Classic benchmarks like Friedman's functions (e.g. y = 10sin(πx1x2) + 20(x3 - 0.5)^2 + 10x4 + 5x5)
Original functions like 10x + sin(5πx) + cos(6πx)
Functions generated by random neural networks
Fitting curves to non-numeric inputs (symbols)
For each task, the language models had to predict outputs from input-output pairs in their "context window", without any gradient updates or backpropagation. Basically, no peeking at the answer key or getting hints - they had to infer the relationship cold.
As a benchmark, the researchers also ran a bunch of classic models on the same tasks:
Linear regression (with L1/L2 regularization)
Polynomial regression
Multilayer perceptrons (neural networks)
Tree-based models like random forest and gradient boosting
Kernel-based models like support vector regression
They compared the average mean squared error of the language models and the classic models over 100 runs of each task (with 50 data points each).
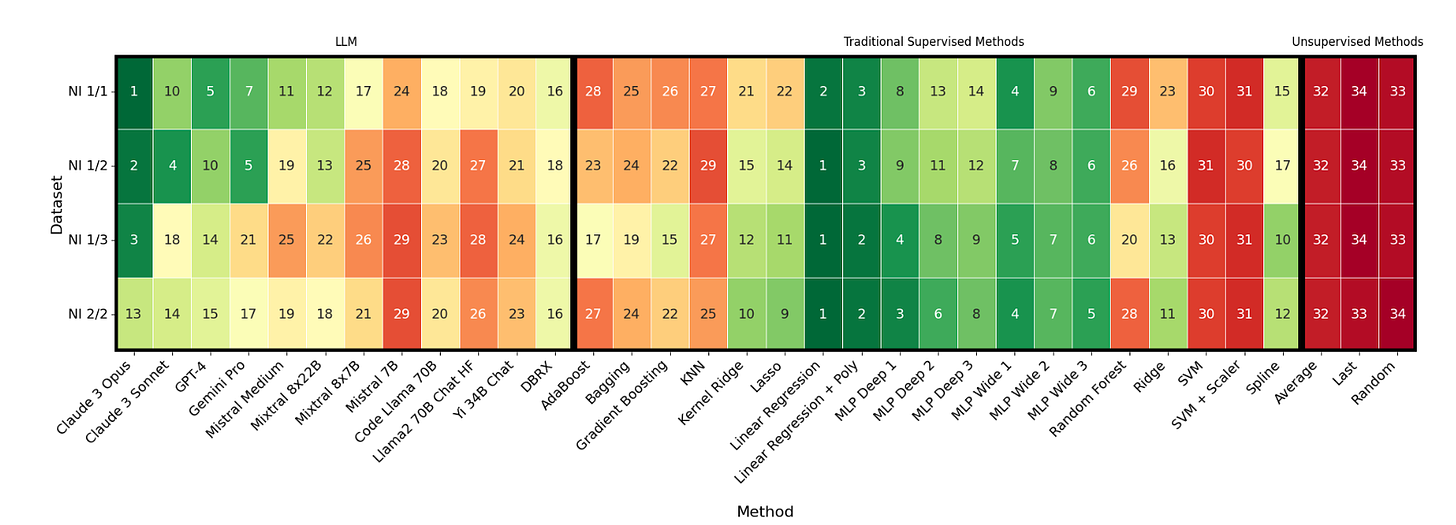
“Figure 3: The rank of each method investigated over all four linear regression datasets. Rankings are visually encoded with a color gradient, where green means better performance (higher ranks) and red indicates worse performance (lower ranks). Notably, very strong LLMs such as Claude 3 and GPT-4 consistently outperform traditional supervised methods such as Gradient Boosting, Random Forest, or KNN”
The results? The big language models (GPT-4, Claude, Anthropic) consistently beat workhorses like gradient boosting, random forest and SVMs. In some cases they even tied purpose-built models like polynomial regression.
For example, on a task with 3 input variables but only 1 predictive variable, Claude matched linear regression and crushed gradient boosting. On a nasty nonlinear function with trig terms, Claude beat everything but polynomial regression.
The researchers also looked at learning efficiency - how the models' performance improved with more data points. The error rate (regret) of GPT-4 and Claude dropped sharply as data increased, sometimes approaching the theoretical optimum.
This suggests that language models aren't just memorizing and interpolating, but generalizing patterns efficiently - hallmarks of "meta-learning".
You can find the full results in the Arxiv paper here.
Limitations
There are some caveats. Data contamination is still a possibility - maybe the language models saw similar examples in their original training data. The researchers tried to control for this using multiple random initializations, testing on original functions, and comparing prompts that hint at the function vs neutral ones. But it's hard to fully rule out without the source data.
The classic ML models weren't heavily tuned, so a hand-tweaked specialist model might still win out. And on some tasks (like approximating a neural net) the language models struggled.
But overall, it's robust evidence that big language models can hang with purpose-built models on tricky regression tasks, with much less fuss. It's an existence proof of cross-domain emergence - language skills breeding math skills.
Critical Analysis
This paper is a great example of how valuable it is to test AI models on tasks they weren't explicitly trained for. By throwing a curveball at language models and seeing how they respond, the researchers revealed a hidden depth to these models - an inductive flexibility that hasn't (to my knowledge) been demonstrated before.
At a high level, it challenges the idea that AI progress right now is all about bigger-better-faster narrow models. It shows how even without revolutionary breakthroughs, general intelligence can start to emerge "in the gaps" from the sheer scale of compute and data we're throwing at language models.
It's not human-level math by any means. But it captures something of the human meta-cognitive trick of rapidly bootstrapping from prior knowledge to solve novel problems. It's a hint that intelligence may not be domain-specific - that in learning to process language, an AI can learn to process the world.
The caveats the authors flag are real but (in my view) don't diminish the core insight. Comparing to finely-tuned task-specific models would be instructive, especially on the nonlinear functions. Testing on a wider range of novel domains (causal inference, time series forecasting, differential equations) would clarify how far the generalization goes. Scaling to larger datasets will determine the break-even point vs specialist models.
And data contamination remains the elephant in the room for any study on emergent abilities in large language models. The authors did their due diligence here, but there's always a non-zero chance that some subset of the training data primed the models for this domain. Access to full training corpora and testing on data that post-dates a model would help.
In the end though, I don't think any of these points detract from the key insight - that general language models, through sheer scale and expressivity, are starting to demonstrate non-trivial mathematical problem-solving abilities. It's an important signpost on the road to richer, more open-ended machine intelligence.
Conclusion
Language is a window into general intelligence - this is the tantalizing implication of the new finding that language models can approximate complex mathematical functions.
Traditionally, mathematical problem-solving in AI has been siloed in specialized architectures, painstakingly crafted and trained for a narrow domain. What this study shows is that a general model trained on nothing but next-word prediction can pick up function approximation as an emergent skill.
This could be another breadcrumb on the trail to artificial general intelligence (AGI) - the grand vision of a system that can learn and reason flexibly about anything, like a human. By untangling complex patterns in language, these language models seem to be “learning” (or at least encoding) something deep about how the world works - concepts like similarity, continuity, modularity. The "language of thought".
This study alone isn't going to get us to HAL 9000. The models still struggle with many hard math problems, and their world knowledge is a far cry from a human's. But it's a powerful proof-of-concept that natural language may be sufficient to bootstrap a proto-AGI - an "all-purpose intellectual Swiss Army knife".
If this paradigm bears out, it could lead to a much leaner, more elegant vision of AI than the narrow-expert model. Instead of a huge stack of brittle specialist models, you'd have one big general-purpose language model that can fluidly adapt to any task - absorbing domain knowledge on the fly from written explanations and examples, like a human.
For data science and ML engineering, this could be game-changing. Why waste time selecting and tuning dozens of different model architectures when one big language model could handle everything from data cleaning to feature engineering to model selection? Just describe your problem and your dataset in natural language, and let the language model figure out the rest.
More broadly, this is a glimpse of an AI that can engage in a form of cross-modal reasoning - weaving together language, images, math, and logic in a fluid stream of thought. An AI that doesn't just mimic narrow human skills, but learns at a deeper, more abstract level from the rich world-knowledge encoded in text.
As always, I'm eager to hear your take. Is this study worth talking about? Are its findings significant? What would it take to convince you? Let me know in the comments.
And if you found this breakdown interesting, come hang out with me on Twitter and check out the latest papers on the site – we're digging into the details of the latest AI research every day, and I'd love to hear your perspective. See you there.